Сумма числа ребер и вершин равна 25.какая это пирамида. я знаю что ответ восьмиугольная пирамида,но я вас умоляю напишите как это можно проверить?какому правилу придерживаться? — знания.site
Я знаю что ответ восьмиугольная пирамида,НО Я ВАС УМОЛЯЮ НАПИШИТЕ КАК ЭТО МОЖНО ПРОВЕРИТЬ?КАКОМУ ПРАВИЛУ ПРИДЕРЖИВАТЬСЯ?
Дерево
Не совсем обычное применение пирамидке-оригами нашёл японский дизайнер Макото Ямагути. В декабрьском номере журнала NOA Magazine за 1975 год он опубликовал модель, которую назвал рождественским деревом. Ямагути использовал три последовательно уменьшающихся пирамиды-оригами, сложенные из квадратов 15х15 см, 12х12 см, 8х8 см.
Для этой модели лучше брать бумагу со сторонами одного цвета, иначе изнанка будет видна в нижней части кроны, нарушая целостность изделия.
Верхушка дерева:
- Складываем лист в «Двойной квадрат». Нижний угол совмещаем с правым, то есть, соединяем две красные точки. Проглаживаем складку, которая образовалась по центру. Раскрываем.
- Нижнюю половину поднимаем.
- Повторяем шаги 1 и 2 на обороте.
- Переведём ближний к нам слой справа налево, как перелистывают страницы книги. На обратной стороне модели повторим то же действие, но зеркально. Должна получиться заготовка с двумя клапанами по обоим бокам.
- Повторяем шаги с 1 по 3 в оставшихся секциях.
- Заготовка на этом этапе выглядит, как на рисунке 6а.
Верхний слой складываем и поворачиваем вправо. Продолжаем тянуть лист, пока не соединятся красные точки, а зелёная опустится вниз, образуя выступ. Модуль из плоского становится объёмным.
- Маленький клапан внизу поднимаем и прячем за большим треугольником.
- Повторяем шаги 6 и 7 в остальных секциях пирамиды.
- Могут возникнуть проблемы с последним клапаном, но если приложить усилия, он тоже зафиксируется правильно. Модуль кроны готов. Используем несколько квадратов с разницей в размерах около 2 см, чтобы создать многоярусную конструкцию. Но листы, меньше чем 8х8 см, будет трудно складывать.
Ствол дерева:
- Лист коричневой бумаги, размером 15х15 см, складываем в «Двойной квадрат».
- Поднимаем левую сторону вертикально вверх и сплющиваем.
- Переворачиваем влево две секции. И повторяем шаги 1 и 2 на оставшихся трёх сторонах.
- Теперь перелистываем верхний слой, чтобы не было видно белой изнанки.
Далее складываем ствол аналогично кроне. Только он получается более узким и каждый угол состоит не из одного, а из двух слоёв.
Осталось собрать наше рождественское дерево. Пирамиды из бумаги сделаны таким образом, что соединяются без клея.
Теперь можно пополнить коллекцию оригами-деревьев ещё одним ярким экземпляром.
Пирамида в геометрии – элементы, формулы, свойства с примерами
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
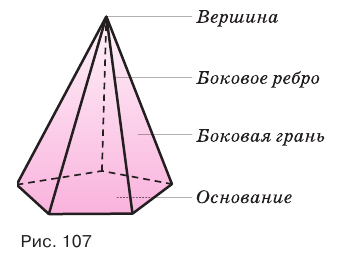
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
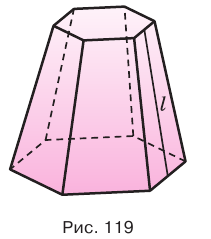
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота 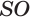
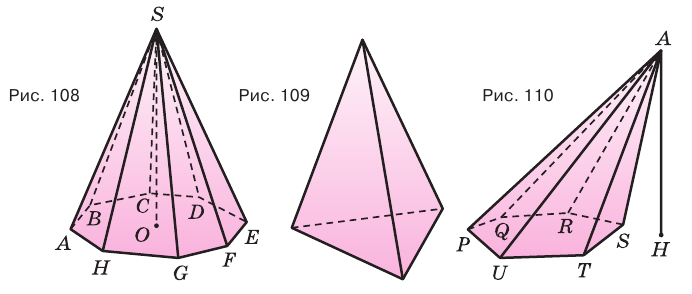
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
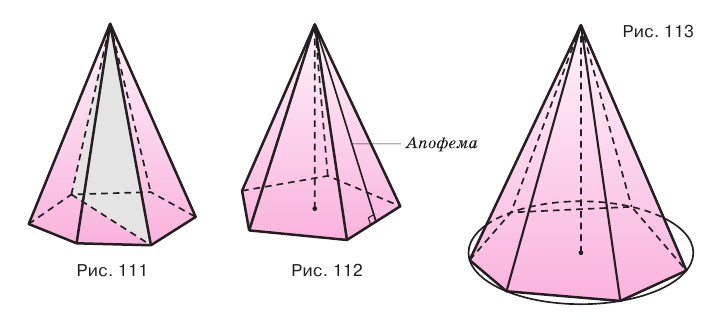
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
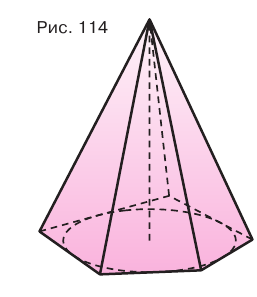
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
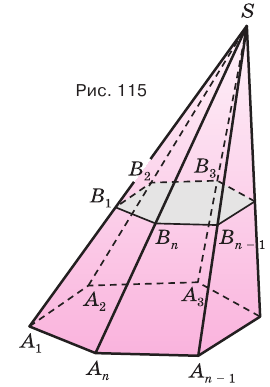
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
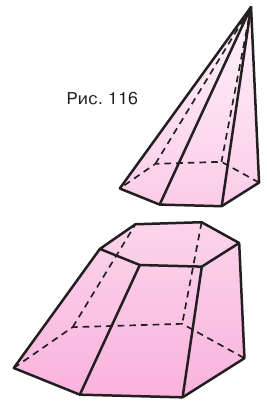
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
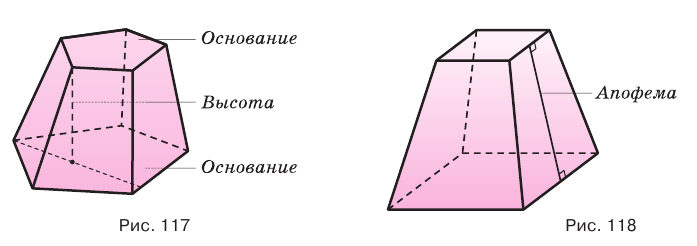
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
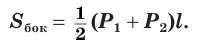
Доказательство:
Пусть есть правильная 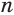 -угольная усеченная пирамида (рис. 119). Пусть
-угольная усеченная пирамида (рис. 119). Пусть 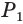 и
и 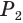 — соответственно периметры нижнего и верхнего оснований и
— соответственно периметры нижнего и верхнего оснований и 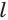 — апофема пирамиды.
— апофема пирамиды.
Боковая поверхность данной пирамиды состоит из 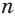 равных трапеций. Пусть
равных трапеций. Пусть 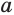 и
и 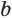 — основания одной из этих трапеций, тогда ее площадь равна
— основания одной из этих трапеций, тогда ее площадь равна 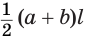 . Учитывая, что боковая поверхность пирамиды состоит из
. Учитывая, что боковая поверхность пирамиды состоит из 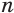 таких трапеций, получим, что
таких трапеций, получим, что
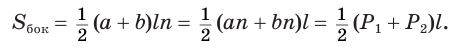
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
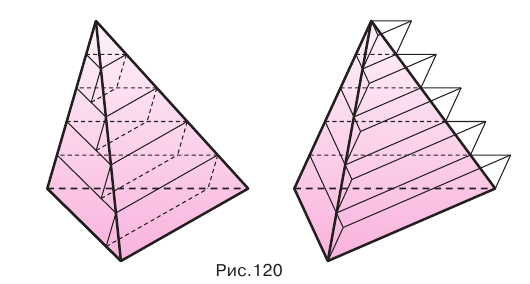
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 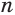 долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на
долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на 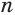 частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
Пусть 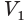 и
и 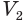 — объемы первой и второй пирамид, a
— объемы первой и второй пирамид, a  и
и  — суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в
— суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в 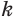 -й части первой пирамиды равновелика призме для
-й части первой пирамиды равновелика призме для 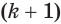 -й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем
-й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем  больше объема
больше объема  на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна
на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна 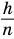 , где
, где 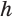 — высота пирамиды (см. рис. 120), т.е.
— высота пирамиды (см. рис. 120), т.е. 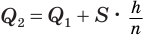 , или
, или 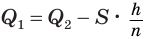 , где
, где 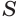 — площадь основания пирамиды. Теперь учтем, что
— площадь основания пирамиды. Теперь учтем, что 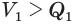 , a
, a 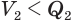 . Поэтому
. Поэтому 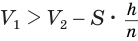 , или
, или 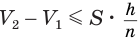 . При увеличении значения переменной
. При увеличении значения переменной 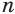 значение выражения
значение выражения 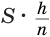 стремится к нулю, а это означает, что
стремится к нулю, а это означает, что 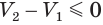 , или
, или

Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство

Из неравенств (1) и (2) следует, что 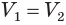 .
.
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
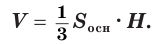
Доказательство:
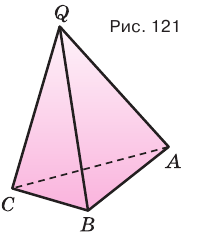
Пусть есть треугольная пирамида  (рис. 121). Достроим ее до призмы
(рис. 121). Достроим ее до призмы  с основанием
с основанием 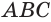 (рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида
(рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида 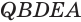 (рис. 122 и 123). Диагональная плоскость
(рис. 122 и 123). Диагональная плоскость 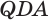 разделяет ее на две пирамиды
разделяет ее на две пирамиды  и
и  , у которых одна и та же высота, проведенная из вершины
, у которых одна и та же высота, проведенная из вершины 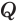 , и равные основания
, и равные основания 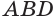 и
и 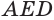 . Поэтому, в соответствии с теоремой 3, пирамиды
. Поэтому, в соответствии с теоремой 3, пирамиды  и
и  равновелики. Сравним пирамиду
равновелики. Сравним пирамиду  с данной пирамидой
с данной пирамидой  . У них равные основания
. У них равные основания 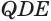 и
и  и высоты, проведенные из вершин
и высоты, проведенные из вершин 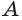 и
и 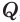 , поэтому эти пирамиды также равновелики. Получается, что все три пирамиды
, поэтому эти пирамиды также равновелики. Получается, что все три пирамиды  ,
,  и
и  равновелики. Поскольку объем призмы
равновелики. Поскольку объем призмы  равен произведению
равен произведению  площади
площади 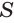 основания
основания  и высоты призмы
и высоты призмы 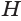 , которая равна высоте пирамиды
, которая равна высоте пирамиды  , то объем пирамиды
, то объем пирамиды  , т. е. третьей части призмы
, т. е. третьей части призмы  , равен третьей доле этого объема, т. е.
, равен третьей доле этого объема, т. е. 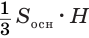 .
.
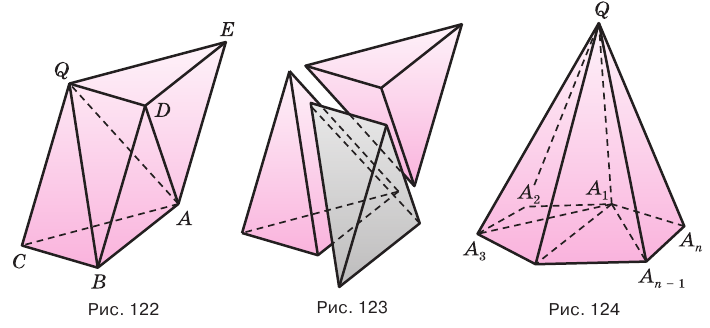
Пусть теперь есть произвольная пирамида 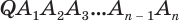 (рис. 124). Через диагонали
(рис. 124). Через диагонали 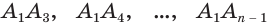 основания
основания 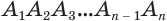 , выходящие из одной вершины
, выходящие из одной вершины 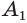 , проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды
, проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды 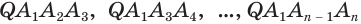 . Поскольку все они имеют общую высоту
. Поскольку все они имеют общую высоту  , то
, то
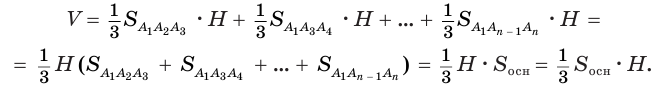
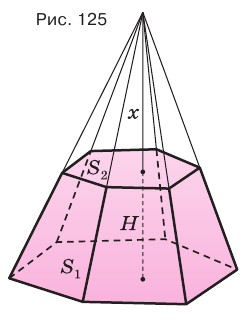
Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 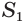 и
и 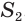 , а высота равна
, а высота равна  (рис. 125).
(рис. 125).
Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 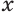 . Искомый объем
. Искомый объем 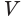 можно найти как разность объемов полной и дополнительной пирамид:
можно найти как разность объемов полной и дополнительной пирамид:
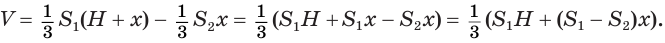
Чтобы найти высоту 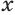 , используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
, используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
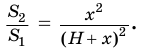
Решим это уравнение, учитывая, что  и
и  — положительные числа:
— положительные числа:
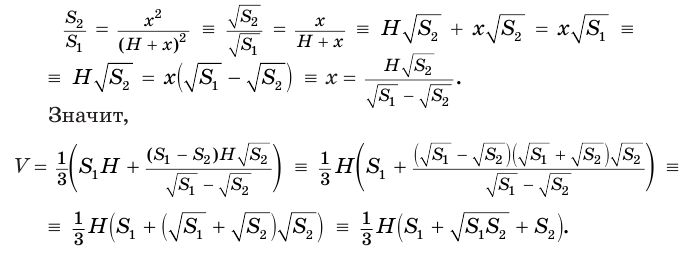
Таким образом, объем 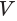 усеченной пирамиды равен третьей доле произведения высоты
усеченной пирамиды равен третьей доле произведения высоты 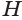 пирамиды и суммы площадей
пирамиды и суммы площадей  и
и  оснований пирамиды и их среднего геометрического
оснований пирамиды и их среднего геометрического 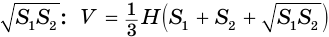 .
.
Тетраэдр
Треугольные пирамидки в технике оригами можно сложить из прямоугольного листа бумаги формата А4, традиционного квадрата или модулей. Схемы сборки для каждой модели отличаются по степени сложности. Самый лёгкий и быстрый вариант ‒ это пирамидка без дна, построенная на базовой форме «Блин».
Пошаговая инструкция:
- Начинаем с изнанки. Намечаем диагонали квадрата. А затем сгибаем к центру четыре угла. Левую часть раскрываем.
- Переворачиваем заготовку. Складываем левую часть пополам. Раскрываем.
- Указанную стрелкой центральную точку тянем вверх. При этом делаем сгибы «горой» по намеченному пунктиру. Левую сторону складываем по серединной линии из шага 2.
- Получается тетраэдр с выступающим треугольным клапаном.
- Заводим «лишнюю» часть внутрь фигуры.
Изготовим большое количество таких модулей-тетраэдров и сложим из них оригинальную абстрактную картину:
Если нужна упаковка для подарка, можно изготовить тетраэдр из трёх модулей. Эффектно раскрываясь, он напоминает цветок, внутри которого ждёт приятный сюрприз. Для этой модели нам понадобятся 3 квадрата, размером 15х15 см.
Пошаговая инструкция:
Каждый лист сгибаем по диагонали. Намечаем середину получившегося треугольника. Располагаем его открытым концом вниз. Правый и левый угол опускаем к вершине.
Готово:
Соединяем модули между собой, вставляя друг в друга.
Третий вариант изготовления пирамиды представлен в видео-инструкции:
Четырёхугольная модель
Пирамида, в основании которой лежит квадрат, была хорошо известна древним цивилизациям. В Египте, Америке, Нубии и Китае возводили культовые сооружения такой формы, которые одновременно служили усыпальницами, храмами и
обсерваториями. Учёные отмечают уникальные свойства геометрических построек, в том числе способность консервировать всё, что попадает внутрь. Так ли это на самом деле, нетрудно проверить, если сделать аналогичную пирамиду из бумаги ‒ конечно, выбрав меньший масштаб.
Пошаговая инструкция:
- С помощью сгибов, делим исходный квадрат пополам во всех направлениях: прямо и по диагонали.
- Теперь складываем лист по направлению, указанному стрелками. Линии, обозначенные штрихпунктиром, сгибаем «горой», а штриховые ‒ «долиной».
- Получаем базовую фигуру «Двойной треугольник». Поворачиваем его открытым краем к себе.
- Складываем правую сторону по пунктиру.
- Выступающую за левую грань часть отгибаем в обратно, выравнивая по центральной оси.
- Закладываем треугольничек, обозначенный стрелкой, внутрь.
- Повторяем шаг 4 слева.
- Отгибаем выступающую часть в обратную сторону.
- Повторяем шаг 6.
- Переворачиваем заготовку. Повторяем шаги 4 ‒ 9 с обратной стороны.
- Сгибаем верхний треугольник вперёд и назад.
- Поворачиваем заготовку на 90°. Сплющиваем и выравниваем дно пирамидки-оригами, одновременно растягивая её в стороны.
Готово:
Альтернативный вариант:
А это ‒ коробочка в форме пирамиды. В неё можно положить сладости на детской вечеринке или небольшой сувенир.







