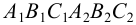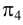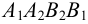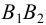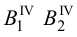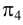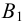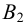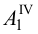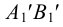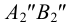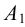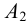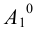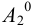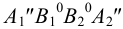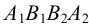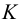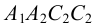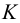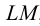Взаимное пересечение поверхностей многогранников
При пересечении поверхностей двух многогранников образуется одна или несколько пространственных замкнутых ломаных линий (в частном случае – плоская ломаная линия).
В зависимости от способа определения элементов линии пересечения (ее сторон или вершин) построение производится путем:
- определения отрезков прямых, по которым грани одного многогранника пересекают грани другого – способ граней;
- определения точек пересечения ребер первого многогранника с гранями второго и ребер второго многогранника с гранями первого – способ ребер.
Выбор способа зависит от расположения многогранников, возможно комбинированное использование обоих способов. На практике используют главным образом способ ребер.
Существуют следующие правила, которыми следует руководствоваться при построении линии пересечения:
- если хотя бы одна проекция ребра многогранника не пересекает проекцию грани другого многогранника, то данное ребро не пересекает этой грани (однако пересечение всех проекций ребра одного многогранника со всеми одноименными проекциями граней другого многогранника не означает, что эти ребро и грань пересекаются);
- проекции линии пересечения располагаются в пределах фигуры, образованной при наложении одноименных проекций двух многогранников;
- отрезок линии пересечения лежит в пределах пересекающихся граней как первого, так и второго многогранника (последовательность соединения точек линии пересечения определяется при помощи вспомогательных диаграмм или таблиц, например при помощи сетки Д.Г.Ананова);
- отрезок линии пересечения считается видимым, если он находится в видимых гранях обоих многогранников.
На рис.113, 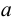
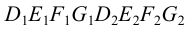
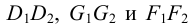
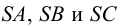
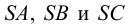
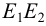
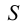
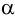
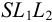
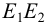
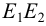
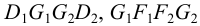
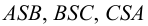
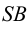
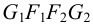
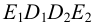
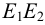
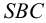
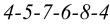
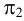
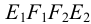
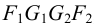
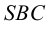
Красота в геометрии.создание моделей правильных многогранников. | образовательная социальная сеть
Содержание
1 Введение
2 Общие указания по изготовлению моделей
3 Платоновы тела
4 Архимедовы тела
5 Заключение
6 Список литературы
7 Приложения
Введение
Ранее меня не слишком увлекала геометрия, да и теперь я не склонна считать этот предмет особо притягательным. Но как оказалось совершенно не обязательно знать теорию, которая изучает и классифицирует многогранники. Можно просто наслаждаться результатом своего труда. Возможно, при виде моделей кто-нибудь спросит: «Какая от них польза?» На это можно ответить так: « А разве все красивое полезно?» Впрочем, можно усмотреть известную пользу, которую приносят модели в качестве декоративных украшений. Ими хорошо украсить комнату или праздничный стол.
Основной целью своей работы считаю научиться делать модели многогранников из бумаги.
Задачи проекта
Знакомство с понятием многогранник.
Изучение видов многогранников.
Знакомство с основными свойствами многогранников.
Поиск исторических фактов.
Исследование возможности бумаги для создания правильных многоугольников и многогранников.
Свою работу я основывала на довольно редкой книге М. Винненджера «Модели многогранников»
Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие в виде вирусов. Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел (подобных пирамидам) наряду с другими видами пластических искусств уходят в глубь веков. Пять правильных тел изучали Теэтет, Платон, Евклид, Гипсикл и Папп.
Возникает вопрос: что такое многогранник? Все термины пришли к нам от древних греков. Влияние знаменитого греческого мыслителя Платона сказалось и на «Началах» Евклида. В этой книге, которая на протяжении веков была единственным учебником геометрии, дано описание «идеальных» линий и «идеальных» фигур. Самая идеальная линия-прямая и самый идеальный многоугольник – правильный многоугольник, иными словами, многоугольник, имеющий равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которые могут ограничить часть плоскости. Интересно, что «Начала» Евклида открываются построением правильного треугольника и заканчиваются изучением пяти правильных тел! Каждый из этих пяти многогранников имеет гранями правильные многоугольники одного типа. В наше время они известны под именем пяти платоновых тел. Тетраэдр, гранями которого являются четыре равносторонних треугольника, можно считать трехмерным аналогом плоского правильного треугольника. Гексаэдр, обычно называемый кубом (шесть граней), имеет квадратные грани; грани октаэдра (восемь граней)- равносторонние треугольники; все грани додекаэдра (двенадцать граней) – пятиугольники; наконец гранями икосаэдра являются двадцать равносторонних треугольников.
Подобно тому как две стороны многоугольника соединяются в вершине, так и любые две грани многогранника соединяются общей стороной – ребром многогранника, сами ребра сходятся в точках называемых вершинами многогранника.
Известно еще множество тел, получивших название архимедовых, или полуправильных многогранников. У них также все многогранные углы равны и все грани- правильные многоугольники, но несколько разных типов. Существует тринадцать полуправильных многогранников, открытие которых приписывается Архимеду, впервые перечислившему их в не дошедшей до нас рукописи. Кеплер первым из современных математиков развил полную теорию этих тел.
Надеюсь, что моя работа заинтересует вас так же, как и меня.
Общие указания по изготовлению моделей
Первое, чему вы должны научиться, прежде чем строить модели многогранников, это точно и аккуратно вычерчивать нужные вам части. Для выпуклых многогранников ими будут только правильные многоугольники с 3, 4, 5, 6, 8 и 10 сторонами. Но следует помнить, что у выпуклых однородных многогранников все рёбра имеют одну и ту же длину. Следовательно, все многоугольники, образующие один многогранник, должны иметь стороны одной длины. А, как легко заметить из чертежей, правильный десятиугольник (декагон), например, значительно больше правильного треугольника с такой же стороной. Это надо всегда иметь в виду при построении моделей и соответственно этому выбирать подходящий масштаб. Подумайте сначала, как вы собираетесь использовать модель и где она будет находиться.
После того как вы со всеми необходимыми предосторожностями сделаете чертежи_ требуемых частей — правильных многоугольников, — лучше всего изготовить трафареты. Для этого наложите чертёж на лист картона или плотной бумаги и проколите оба листа в вершинах многоугольника тонким шилом (или любой достаточной тонкой и острой иглой). После этого соедините по линейке полученные проколы, воспользовавшись острым карандашом. Аккуратно и ровно вырежьте ножницами трафарет, оставляя поля, отстоящие от карандашной линии примерно на 0,5 см. Итак, трафарет готов.
Теперь уже не составит труда изготовить столько его копий, сколько вам требуется. Для этого нужно наложить трафарет на стопку листов картона. (Лучше, если эти листы предварительно закреплены скрепками.) Не следует брать одновременно больше шести листов. При этом, если, например, вы хотите изготовить одинаковое число фигур различных расцветок, имеет смысл сразу же соединять разноцветные листы. После этого вы снова прокалываете вершины многоугольников, пользуясь трафаретом. Обведите его карандашом и затем уберите или же перенесите на чистый лист. Таким способом вы сделаете столько проколов, сколько сочтёте нужным.
Следующий ваш шаг — нарезать стопку картона по только что нанесённой обводке. Обязательно проследите, чтобы листы картона были надёжно соединены скрепками. Обычно при такой нарезке листы слегка прогибаются и разрез сдвигается, но пусть это вас не пугает — оставленные поля дают нам достаточный запас. Впрочем, после того как заготовки нарезаны, их несложно подравнять, подрезав края каждой из них в отдельности. Теперь каким-нибудь острым инструментом, например кончиком циркуля, нанесите прямые бороздки по сторонам многоугольника. При этом не забывайте пользоваться угольником или линейкой. Итак, вы проводите прямые бороздки, которые соединяют проколотые точки. После этого уже нет нужды размечать линии карандашом — границы достаточно заметны. Вот теперь самое время аккуратно подравнять ножницами края заготовки. Как мы уже говорили, каждую из них лучше обработать в отдельности. Срежьте уголки заготовки так, чтобы разрез проходил точно через прокол. После этого наши поля превратились в наклейки, и их следует отогнуть. Проведённые бороздки позволяют сделать это легко и точно. При помощи наклеек заготовки склеиваются друг с другом. Если многоугольник-заготовка имеет острые углы, после отгибания следует дополнительно подрезать наклейки. Этого не стоит делать заблаговременно, иначе операция усложнится. Со временем вы научитесь с лёгкостью подгонять все части, причём будете делать это чрезвычайно аккуратно. Помните основное правило: для склеивания надо оставлять как можно больше места и срезать столько, сколько необходимо, чтобы наклейки не мешали одна другой и граням вблизи вершин.
Можете воспользоваться любым клеем, лишь бы он не коробил заготовки. Но вообще-то постарайтесь выбрать тот, что быстрее схватывает. Процедура склеивания чрезвычайно проста: вы наносите клей на одну из наклеек, после чего прижимаете наклейки друг к другу и немного их двигаете, чтобы клей равномерно распределился по поверхностям. Заготовкам следует придать правильное положение, дожидаясь, пока клей подсохнет. В вашей работе время от времени надо пользоваться пинцетами; они особенно полезны при завершении работы, когда модель приобретает окончательную форму. На собственном опыте вы вскоре убедитесь, что способ изготовления моделей склеиванием отдельных граней, который мы предлагаем, позволяет получить на редкость жёсткие конструкции. Это объясняется тем, что наклейки, оставляемые нами на каждой грани, служат дополнительными рёбрами, придающими жёсткость каждому ребру модели. Вот почему лучше следовать нашему правилу и оставлять наклейки с каждой стороны любой заготовки. Конечно, возможны иногда отступления, но лишь в крайних случаях. В основном же для любых выпуклых многогранников лучше оставлять все наклейки.
Мы начали с выпуклых однородных многогранников. Их модели проще всего изготовить. Говоря о раскраске моделей, мы ориентировались на советы данные в книге. Но со временем поняли, что найти подходящий (тонкий) цветной картон или же достаточно плотную цветную бумагу проблематично, и перешли на бумагу «Снегурочка». Но она подходит только в случае изготовления моделей небольших размеров. Но все-таки если изготавливать цветную модель, то грани многогранника, имеющие общее ребро, должны быть окрашены в разные цвета.
Так же хотелось бы дать пояснения к приложению. Развертки правильных многогранников в натуральную величину давать не целесообразно, так как они делаются элементарно. Причем не обязательно делать из развертки, можно склеивать каждую грань отдельно. Для полуправильных в приложения вынесены только развертки предложенные автором книги. Если развертки нет, значит многогранник собирается из отдельных граней.
Платоновы тела
Тетраэдр
Простейшим среди многогранников является тетраэдр. Его четыре грани — равносторонние треугольники. Четыре — это наименьшее число граней, отделяющих часть трёхмерного пространства. Тем не менее тетраэдр обладает многими свойствами, характерными для однородных многогранников. Все его грани суть правильные многоугольники, причём каждая отделяется ребром в точности от одной грани. Все многогранные углы тетраэдра также равны между собой. Модель тетраэдра можно сделать, пользуясь одной развёрткой, на которой будут расположены все четыре треугольные грани. Однако в этом случае все грани будут одного цвета. Подобным же образом все выпуклые многогранники можно сделать с помощью одной развёртки и тем самым одноцветными .Если же вы хотите сделать модель тетраэдра (как и любого многогранника) разноцветной, следует приготовить развёртки для каждого типа грани в виде отдельного многоугольника. Для тетраэдра вам понадобится всего один трафарет в виде равностороннего треугольника.
Сделайте четыре заготовки разного цвета — например. Ж, С, О и К. Не забудьте оставить наклейки с каждой стороны, как показано. Теперь склейте все четыре заготовки вместе в положение, показанное на картинке. Соедините не склеенные боковые грани и склейте вначале только две из них между собой. Затем наложите клей на оставшиеся наклейки и приклейте последнюю грань, как бы закрывая коробку. Дальнейшее сделают внутренние напряжения в модели, ваши пальцы, приложенные к её ребрам, и высыхающий клей.
Октаэдр
Октаэдр — это многогранник, гранями которого являются восемь равносторонних треугольников. Так как его противоположные грани лежат в параллельных плоскостях, то можно превосходно обойтись всего четырьмя красками. Модель этого многогранника вы начинаете делать, склеивая четыре треугольника, как показано на рисунке справа. После того как вы склеите между собой грани 1 и 4, в ваших руках окажется правильная четырёхугольная пирамида без квадратного основания. Эта часть составляет ровно половину модели.
Вторая половина энантиоморфна первой. Тем не менее проще продолжить работу в такой последовательности: сначала приклейте наклейки четырёх оставшихся треугольников к соответствующим наклейкам на сторонах квадратного основания. (Проследить, чтобы противоположные грани октаэдра имели один и тот же цвет, нетрудно.) Затем последовательно склейте наклейки соседних граней, снова закрывая модель последним треугольником, как крышкой.
Гексаэдр (куб)
Несомненно, куб, или, как его иногда называют математики, гексаэдр — самый общеизвестный и широко используемый. многогранник. Все шесть его граней — квадраты, сходящиеся по два вдоль каждого ребра и по три в каждой вершине. Вы можете начать постройку модели куба, выбрав один квадрат и присоединив к нему четыре других. Затем вы склеите наклейки соседних боковых граней, причём склеенные попарно наклейки вновь образуют как бы жёсткий скелет многогранника. Остаётся добавить последнюю грань, и это действие уже с полным правом можно будет уподобить закрыванию ящика крышкой.
Возможно, что в своей простоте куб не самый привлекательный многогранник. Но он обладает несколькими удивительными свойствами в отношении других платоновых и некоторых архимедовых тел. А объединение пяти кубов можно поместить в додекаэдр, и при этом получается очень красивая модель.
Икосаэдр
Икосаэдр -одно из пяти платоновых тел, по простоте следующее за тетраэдром и октаэдром. Их объединяет то обстоятельство, что гранями каждого являются равносторонние треугольники. При изготовлении модели икосаэдра можно выбрать любую из двух эффектных возможностей распределения пяти цветов. Во-первых, икосаэдр может быть раскрашен так, что у каждой вершины встретятся все пять цветов (правда, в таком случае противоположные грани не будут окрашены одинаково). Другой способ обеспечивает противоположным граням одинаковые цвета, зато у каждой вершины, за исключением двух полярных, будет повторяться по кругу один цвет. Обе раскраски очень интересны и для наших целей полезны, ибо многие описанные ниже однородные многогранники имеют икосаэдральную симметрию. Быть может, по этой причине вы сочтёте нужным впоследствии иметь две модели икосаэдра с разной раскраской. Обе модели можно строить, исходя из одного и того же начального расположения пяти равносторонних треугольников, как показано в приложении 3. Они образуют невысокую пятиугольную пирамиду без основания. К сторонам её основания приклейте следующие пять треугольников, руководствуясь той или иной таблицей раскраски. Между ними вы приклеите по одному треугольнику — это сделать несложно, если обратить внимание на то, что в каждой вершине сходятся пять граней. Завершая модель, приклейте последние пять треугольников.
Додекаэдр
В известном смысле додекаэдр представляет наибольшую привлекательность среди платоновых тел, соперничая с икосаэдром, который почти ему не уступает (а быть может, в чём-то и превосходит). Модель этого многогранника можно сделать четырёхцветной двумя способами; если же воспользоваться для раскраски шестью цветами, то противоположные грани легко сделать одноцветными.. Построение модели вы начинаете с приклеивания пяти разноцветных
пятиугольников — скажем, Ж, С, О, К, З — к одному центральному пятиугольнику, например белого цвета (Б). После этого вам следует склеить цветные пятиугольники между собой — и половина дела сделана. Остаётся подклеить остальные грани додекаэдра к уже сделанной половине таким образом, чтобы противоположные грани были одноцветными.
На рисунке в приложении 4 показана четырёхцветная раскраска додекаэдра. Можно воспользоваться и энантиоморфным порядком цветов. Иногда удобнее обращаться именно к такой раскраске — особенно для моделей, имеющих симметрию додекаэдра.
На этом заканчиваем построение пяти правильных многогранников и переходим к архимедовым телам их 13.
Архимедовы тела
Усечённый тетраэдр
Эту же модель можно построить так. Сначала вы делаете чашу в форме тетраэдра, развёртка которой показана на рисунке приложения 5. Дно чаши будет треугольным, а стенки — шестиугольными. При этом соединённые наклейки превратятся в жёсткие ребра по углам чаши, находящиеся внутри неё. Затем вы склеиваете треугольники и шестиугольник между собой (лучше оставить одну треугольную грань напоследок, крепко приклеив её только одной стороной) и закрываете отверстие, как закрывают крышку ящика. Такой способ рекомендуется применять при построении всех моделей.
Усечённый октаэдр
Построение модели вы начинаете, окружая один шестиугольник четырёхугольными и шестиугольными гранями, одна за другой, как показано на рисунке справа. Склеив соседние грани, вы получите чашу, образующую ровно половину модели. Приложение 6
После этого вам не составит труда подклеить остальные части — нужно только проследить за тем, чтобы противоположные грани были одного цвета. В последнюю очередь надо подклеить какой-нибудь квадрат. Вряд ли следует вам напоминать, что до тех пор, пока вы его не приклеите, модель будет легко деформироваться. После завершения работы модель окажется весьма жёсткой — это характерно для всех выпуклых многогранников.
Усечённый гексаэдр (куб)
Изготовление этой модели можно начать с того, чтобы окружить один восьмиугольник соседними треугольниками и восьмиугольниками, как показано в приложении 7. Склеив между собой наклейки соседних восьмиугольников, оставьте треугольные отверстия, которые потом заклейте треугольниками. Как и в предыдущих моделях, хорошенько приклейте одну сторону треугольной грани, а затем закройте отверстие треугольной крышкой. Всё это нетрудно сделать, пока модель не закрыта и имеется доступ внутрь.
В последнюю очередь вы приклеиваете жёлтый (Ж) восьмиугольник, а четырьмя красными (К) треугольниками закрываете углы. Обратите внимание: по сравнению с предыдущими моделями изготовление этой модели требует от вас большей ловкости и аккуратности. Но мы не сомневаемся, что, если вы на этом не остановитесь, а продолжите работу по построению моделей, нужные навыки придут к вам сами.
Усечённый икосаэдр
Начните с белого (Б) пятиугольника, обклеив его пятью разноцветными шестиугольниками — Ж, С, О, К, З. Внимательно проследите за каждым новым кольцом шестиугольников, добавляя всякий раз белый пятиугольник в его центр. Таким способом вы легко подклеите недостающие пять колец шестиугольников. Разумеется, каждый шестиугольник будет входить в три таких кольца. Законченная модель весьма привлекает чередованием разноцветных пяти- и шестиугольных граней.
Усечённый додекаэдр
Гранями этого многогранника являются правильные треугольники и десятиугольники. Здесь для десятиугольных граней мы можем вновь воспользоваться четырёхцветной раскраской додекаэдра, сделав все треугольники, например, зелёного цвета. Исходный красный (К) десятиугольник окружите последовательно десятиугольниками следующих цветов: Ж, C, О, C, О, а все треугольные отверстия закройте зелёными (З) треугольниками. Следующие пять десятиугольников будут иметь цвета: К, Ж, К, С, Ж. При этом первый из них (К) надо подклеить к тому оранжевому (О) десятиугольнику, который расположен между двумя синими (С) десятиугольниками. После того как вы это сделали, приклейте на свои места остальные треугольники.
Эта модель не выглядит особо привлекательной, возможно, потому, что площади треугольников слишком малы по сравнению с площадями десятиугольников. Исходя из этого, при изготовлении модели необходимо как-то укрепить или усилить десятиугольные грани изнутри, иначе они будут легко сминаться. Для этой цели лучше всего воспользоваться более плотным картоном. Впрочем, если модель не слишком велика, надобности в таком усилении нет.
Кубооктаэдр
Само название многогранника указывает на некую близость его к кубу и к октаэдру. Такая близость существует в действительности. Шесть квадратных граней этого многогранника принадлежат граням некоторого куба, тогда как восемь треугольных граней принадлежат граням октаэдра. Если впоследствии вы захотите сделать модель соединения этих двух платоновых тел, то на ней вы отчётливо увидите, что кубооктаэдр является их общей частью.
При изготовлении этой модели можно использовать для раскраски квадратов те же цвета, что и для граней куба, а все треугольные грани сделать одноцветными.
Прежде всего подклейте к одному треугольнику три квадрата, как это показано в приложении 8. Затем с помощью ещё трёх треугольников склейте подобие чаши с треугольным дном и стенками, составленными из квадратов и треугольников, которые чередуются между собой. По окончании этой работы вы получите половину модели. После этого вам будет нетрудно подклеить недостающие грани. Проследите только за тем, чтобы противоположные квадратные грани имели один и тот же цвет.
Важнейшим свойством этого многогранника является то, что он имеет грани двух типов, причём каждая грань одного типа соседствует только с гранями другого типа. Многогранники, обладающие этим свойством, называются квазиправильными.
Икосододекаэдр
Икосододекаэдр, подобно кубооктаэдру, являет собой квазиправильный комбинированный многогранник. Его также можно рассматривать как общую часть соединения двух тел — икосаэдра и додекаэдра. При раскраске икосододекаэдра можно ограничиться пятью цветами: если сделать все треугольные грани зелёными (З), то остальными четырьмя цветами можно раскрасить пятиугольные грани, подобно тому как раньше мы раскрашивали додекаэдр.
Вы можете начать работу, подклеив к исходному синему (С) пятиугольнику пять зелёных треугольников. Следующие пять пятиугольников приклеиваются так, чтобы каждый из них двумя соседними гранями соединялся с двумя треугольниками. Цвета для пятиугольников — О, К, Ж, К, Ж. Подклеив в промежутки между пятиугольниками недостающие пять треугольников, мы получим ровно половину модели. При этом оставшиеся наклейки будут находиться по сторонам правильного десятиугольника. Продолжая работу, вы будете подклеивать к ним треугольники и пятиугольники в чередующемся поряд-ке.
Начните с треугольных граней, подклеив их к свободным сторонам пятиугольников. Затем подклейте оранжевый (О) пятиугольник так, чтобы его вершина совпала с вершиной того жёлтого (Ж) пятиугольника, который находится между двумя красными (К). Порядок раскраски пятиугольников таков: О, С, О, К, С. Последний жёлтый (Ж) пятиугольник добавляется после того, как подклеена часть оставшихся треугольников. Изготовление модели заканчивается как обычно.
На модели ясно видны шесть различных «экваториальных» поясов, образованных рёбрами многогранника. Это свойство используется при построении моделей некоторых невыпуклых однородных многогранников.
Ромбокубооктаэдр
Название многогранника и на этот раз объясняет его происхождение. Множество квадратных граней ромбокубооктаэдра разбивается на два подмножества, каждому из которых можно отнести свой цвет. Для треугольников естественно выбрать третий цвет.
При построении этой модели можно начать со склейки показанных в приложении 9 частей, которые образуют неглубокую чашу с восьмиугольным верхним краем. К свободным наклейкам подклеиваются квадраты, причём их раскраска должна чередоваться в порядке, который указан второй строкой таблицы раскраски. Например, каждый красный (К) квадрат «экваториального» пояса подклеивается к синему (С) треугольнику, а каждый жёлтый (Ж) квадрат — к красному (К) квадрату. После этого легко закончить модель, подклеивая части по отдельности и продолжая чередовать цвета соседних квадратов. В результате получается довольно красивая модель, хотя её гранями являются лишь правильные треугольники и квадраты.
Следует отметить, что, повернув одну восьмиугольную чашу ромбокубооктаэдра на угол 45° по отношению ко всему телу, можно получить многогранник, называемый псевдоромбокубооктаэдром. Это новое тело имеет равные многогранные углы. Однако оно не относится к архимедовым телам, ибо в нём перепутаны квадратные грани, имеющие кубическое и ромбическое происхождение1
1 Этот многогранник не был известен на протяжении двух тысяч лет, видимо, именно потому, что его нельзя получить при помощи описанной выше процедуры ромбического усечения. Однако его, очевидно, следует включить в список архимедовых (или полуправильных) тел, если характеризовать эти тела не просто как известные Архимеду.Любопытно отметить, что в конце 50-х — начале 60-х годов прошлого столетия «брешь» в стройной теории архимедовых тел независимо обнаружили сразу несколько математиков в разных странах. Первым здесь, видимо, был советский учёный В. Г. Ашкинузе (1957); западные же учёные в этой связи чаще ссылаются на публикацию югославского математика С. Билинского от 1960 года.
Ромбоикосододекаэдр
Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Простейшее и наиболее естественное распределение красок на модели этого многогранника сводится к тому, что каждый из трёх типов граней получает свой цвет. Например, все треугольники — жёлтый (Ж), все квадраты — синий (С) и все пятиугольники — оранжевый (О). Вы можете подряд обклеивать каждый пятиугольник квадратными гранями, каждые две из которых будут связаны промежуточной треугольной гранью.
Ромбоусечённый кубооктаэдр
Этот многогранник, известный также под названием усечённого кубооктаэдра, как и предыдущий, устроен так, что допускает простую раскраску: три разных цвета служат для окраски пар противоположных восьмиугольных граней, четвёртый цвет — для всех шестиугольников, пятый — для всех квадратов. Как обычно, приступая к построению модели, вы составляете в чашу исходные заготовки, показанные в приложении 10. После этого подклеиваете четыре восьмиугольника в соответствии с указаниями во второй строке таблицы раскраски. Завершить работу не составляет никакого труда.
Эта модель несколько более запутанная и сложнее в изготовлении, чем предшествующие, но вместе с тем и более интересная.
Ромбоусечённый икосододекаэдр
Этот многогранник часто называют также усечённым додекаэдром. Красивую раскраску его модели можно получить самым простым способом: все десятиугольники пусть будут одноцветными, скажем, жёлтыми (Ж), все шестиугольники — синими (С) и все квадраты — оранжевыми (О).
Для построения модели вам предстоит выполнить уже знакомую последовательность действий: окружите каждый десятиугольник чередующейся последовательностью шестиугольников и квадратов, образующих кольцо. Тем самым любые два десятиугольника будут отделены друг от друга подобным кольцом, причём каждая квадратная грань будет принадлежать в точности двум разным кольцам. Близкие к этому многограннику тела найдутся также среди н е в ы п у к л ы х многогранников.
Поскольку ромбоусечённый икосододекаэдр имеет десятиугольные грани, то для обеспечения необходимой жёсткости модели эти грани следует делать из более плотного картона. Однако при небольших размерах модели требуемая жёсткость обеспечивается автоматически.
Курносый куб
Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причём эти квадратные грани курносого куба окажутся как бы слегка повёрнутыми по отношению к соответственным граням куба. К каждой стороне квадрата примыкает треугольная грань, поэтому квадрат выглядит окружённым треугольниками. Таких треугольников всего 24. Кроме того, восемь дополнительных треугольников закрывают отверстия, остающиеся после склеивания предыдущих заготовок.
Подобное строение многогранника подсказывает следующую его раскраску. Три противоположных квадрата раскрашиваются тремя красками. Прилегающие к каждому квадрату треугольники одноцветны, но в силу соблюдения основного принципа раскраски карт этот цвет меняется в зависимости от раскраски соответствующего квадрата. Для раскраски треугольников используются те же три цвета, что и для квадратов. Наконец, четвёртым цветом отмечаются все восемь дополнительных треугольников.
При изготовлении модели следует пользоваться таблицей (приложение 11), указывающей распределение цветов для первых трёх частей модели. Эти части затем склеиваются вместе, причём в качестве связок между разноцветными треугольниками используются дополнительные красные (К) треугольники. Склеенные подобным образом три части образуют половину модели. Точно так же выполняется и вторая половина работы, нужно только проследить за тем, чтобы противоположные квадратные грани модели имели одинаковую раскраску.
Курносый додекаэдр
Этот многогранник находится в таком же отношении к правильному додекаэдру, в каком курносый куб находится к правильному гексаэдру (кубу). Чтобы раскрасить модель, возьмите все пятиугольники одного цвета, скажем зелёного (З). Заметьте, что каждый из них окружён пятью треугольниками и всем таким треугольникам можно было бы дать один цвет. Однако допустима и другая раскраска, при которой у каждой пятёрки треугольников будет свой цвет, соответствующий четырёхцветной раскраске додекаэдра. При этом дополнительные связующие треугольники также можно сделать зелёными.
* * *
Курносый додекаэдр — последний из семейства выпуклых однородных многогранников.
Заключение
Первоначальная цель была смоделировать очень красивую звездчатую (есть и такие!) форму многогранника, но в процессе работы я поняла, что без азов у меня ни чего не выйдет. Поэтому свою работу посвятила начальному этапу, то есть изготовлению пяти правильных и тринадцати полуправильных многогранников. Так же хотелось заинтересовать более обширный круг людей, рассказать о том, что сама узнала в процессе работы. Это удалось на неделе математики. Где провели мастер-класс по изготовлению правильных многогранников. Из презентаций узнали о многогранниках в истории, природе, и многом другом. На память изготовили календарь в форме додекаэдра(приложение 12)
В процессе сбора информации о моделях многогранников я узнала о еще одном способе изготовления моделей, с помощью оригами .На основе правильных многогранников устроены кусудумы-очень красивые модели изготовленные с помощью техники оригами. Кроме того, модели можно изготавливать из подручных материалов, таких например как коктейльная трубочка.
Я же решила не останавливаться на достигнутом и продолжать работать над моделями представленными в книге М.Винненджера. Тем более, что осталось их не так уж и мало: 48 звездчатых форм и 53 невыпуклых однородных многогранника. Боюсь только, одной мне с этой работой не справиться, но, думаю, в единомышленниках недостатка не будет. И совместными усилиями мы подтвердим слова Льюиса Кэрролла: «Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Литература
1 М.Виненнджер «Модели многогранников» изд. «Мир» Москва 1974 г.
2
Приложения
1
2 Октаэдр
3
Икосаэдр
4 Додэкаэдр
5
Усеченный тетраэдр
6
Усеченный октаэдр
7
Усеченный гексаэдр
8 Кубооктаэдр
9
Ромбокубооктаэдр
10 Ромбоусеченный кубооктаэдр
11 Курносый куб
Пересечение плоскости и прямой с многогранниками
При пересечении многогранника плоскостью в общем случае получается плоский многоугольник 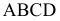
Плоскую фигуру, полученную от пересечения многогранника плоскостью, называют сечением
Рассмотрим несколько примеров.
На рис. 8.5 построены проекции фигуры сечения наклонной трехгранной призмы фронтально проецирующей плоскостью 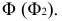
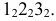
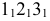
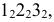
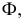
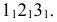
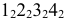
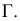
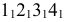
Если многогранник пересекает плоскость общего положения, то для определения линии пересечения необходимо воспользоваться некоторыми дополнительными вспомогательными построениями. Эти построения можно выполнятъ двумя способами:
- а) метод ребер – нахождение точек пересечения ребер многогранника с плоскостью, т.е. нахождение вершин многогранника, получающегося в сечении;
- б) метод граней – нахождение линий пересечения граней многогранника с секущей плоскостью, т.е. нахождение сторон сечения
Так, на рис. 8.7. линия пересечения призмы 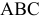
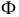
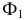
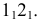
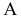
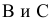
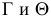
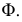
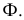
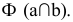
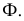
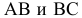
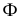
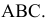
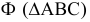
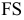
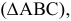
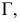
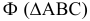
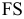
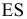
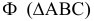
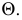
Прямая линия может пересекать поверхность многогранника в двух точках при условии, что многогранник выпуклый. Решение этой задачи основано на схеме определения точки пересечения прямой с плоскостью и распадается на три этапа:
- через заданную прямую проводится вспомогательная плоскость;
- строится проекция фигуры сечения многогранника;
- определяются точки пересечения прямой с контуром сечения.
На рис. S.11 построены точки 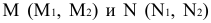
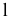
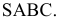
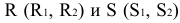
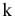
Развертка поверхности конуса
Разверткой боковой поверхности прямого кругового конуса является сектор, радиус которого равен длине образующей конуса 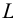
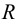 Пример 25. Построить развертку прямого кругового конуса и нанести на нее линию пересечения фронтально-проецирующей плоскостью
Пример 25. Построить развертку прямого кругового конуса и нанести на нее линию пересечения фронтально-проецирующей плоскостью 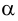 (рис.110).1. Основание конуса разобьем на
(рис.110).1. Основание конуса разобьем на 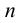
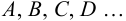
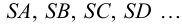
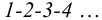
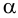
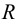
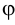
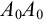
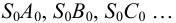
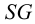
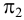
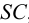
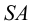
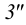
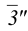
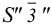
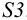
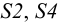
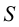
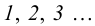
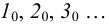
В общем случае для построения развертки поверхности наклонного конуса в него вписывают пирамиду, ребра которой равны отрезкам образующих конуса, и строят развертку поверхности этого многогранника. Построенные на развертке вершины основания пирамиды соединяют по лекалу плавной кривой линией, а крайние точки связывают с вершиной конуса отрезками прямой линии. Построенная развертка тем точнее, чем больше граней у пирамиды, вписанной в конус.
Для получения полной развертки поверхности конуса развертку боковой поверхности дополняют фигурой, лежащей в основании конуса. Если основание конуса не параллельно плоскости проекций и не лежит в ней, то для построения его на развертке первоначально необходимо найти натуральную величину этой фигуры.
На рис.111 дан пример построения развертки наклонного кругового конуса. В конус вписана шестиугольная пирамида, основанием которой является правильный шестиугольник 
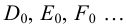
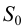
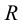
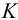
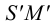
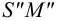
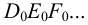
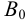
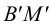
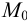
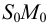
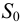
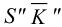
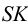
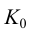
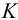
Развертка поверхности пирамиды
Развертка полной поверхности 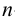
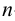
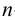 методом треугольников, который сводится к определению натурального вида треугольников, являющихся гранями пирамиды.На рис.106 показано построение развертки наклонной треугольной пирамиды
методом треугольников, который сводится к определению натурального вида треугольников, являющихся гранями пирамиды.На рис.106 показано построение развертки наклонной треугольной пирамиды 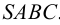
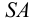
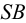
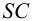
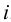
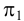
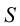
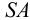
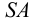
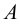
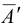
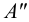
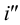
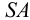
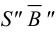
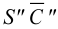
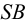
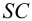
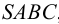
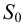
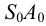
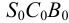
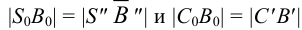
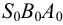
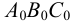
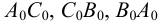
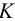
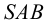
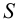
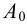
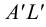
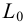
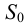
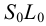
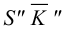
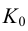
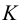
Развертка поверхности призмы
Развертка поверхности прямой призмы строится весьма просто: развертка ее боковой поверхности представляет собой ряд прямоугольников с общими сторонами. В этом случае построение развертки сводится к определению натуральных величин основания призмы и одного ребра.
Развертка полной поверхности 
Для построения развертки наклонной призмы можно использовать два способа – нормального сечения и раскатки. Строго говоря, метод треугольников также может быть применен для построения развертки поверхности призмы, у которой все грани предварительно разбиты на треугольники.
Однако на практике построение развертки призмы этим методом проводится крайне редко в связи с необходимостью выполнения многочисленных построений. Если основания призмы проецируются с искажением, то для построения развертки следует предпочесть метод нормального сечения.
Метод нормального сечения (сечения, перпендикулярного ребрам призмы) состоит из следующих построений:
- поверхность многогранника пересекают плоскостью, перпендикулярной его ребрам;
- определяют натуральную величину нормального сечения;
- находят натуральную величину ребер многогранника;
- на свободном месте чертежа контур нормального сечения развертывают в отрезок прямой;
- через концы отрезков проводят перпендикуляры, на которых откладывают натуральные величины отрезков ребер;
- концы перпендикуляров соединяют;
- к построенной развертке боковой поверхности призмы пристраивают основания.
На рис.107 и 108 показано построение развертки треугольной наклонной призмы 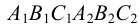
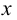
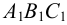
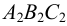
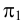
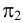
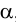
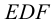
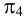
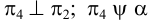
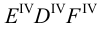
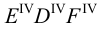
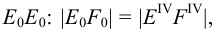
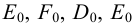
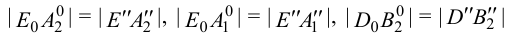
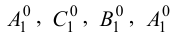
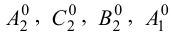
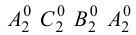
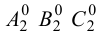
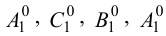
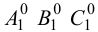
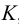
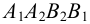
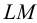
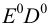
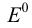
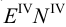
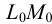
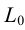
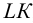
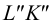
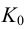
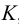 Метод раскатки состоит в том, что призму последовательно вращают вокруг ее ребер до совмещения граней с плоскостью чертежа. Пример построения развертки поверхности призмы
Метод раскатки состоит в том, что призму последовательно вращают вокруг ее ребер до совмещения граней с плоскостью чертежа. Пример построения развертки поверхности призмы